RogerBW's Blog

Since the data are available, I thought I'd calculate the population-weighted centre of Great Britain.

The first thing to do is gather the data, of course. I decided to leave out Northern Ireland, because distance is less meaningful as a proxy for travel time when there's a different mode of travel involved in crossing it. (Also because the data for Northern Ireland are only available by "settlement", not by postal code or anything else readily convertible to coordinates.)

Indeed, converting to coordinates is the hard bit. However, thanks to Code Point Open, I can get a reasonably comprehensive list of postal codes in the UK, and map them to Ordnance Survey easting/northing coordinate pairs. Though I do therefore need to attribute this blog post:

Contains OS data © Crown copyright 2012

Contains Royal Mail data © Royal Mail copyright and Database right 2012

(I used a version of Code Point Open that I'd downloaded in 2012, which since I was using 2011 census data seemed like a sensible approach to take. They don't make older versions available on the site.)

So that gave me a way of converting post codes into coordinates (and I decided to calculate in easting/northing coordinates so as to keep the maths simple and not to have to allow for spherical trigonometry; I get enough of that when I'm doing naval wargaming). Next to get a set of post codes.

For England and Wales I used the Population and Headcount Estimates from the 2011 census, table 1 only. This gave me a list of postcodes and the usual number of residents at each. Of the 1,308,780 postal codes given, 442 did not appear in the 2012 Code Point Open data, so I have no information for 6,745 out of the 56,075,912 people listed. That seems like an acceptable error.

For Scotland I used the Data Warehouse "Release 2a Standard", which includes data at Postcode Sector resolution rather than full postal code. This means one gets data by partial codes such as "AB12 4". (Just to make things harder, some sectors are split anyway - thus there's "AB12 3 (part) Aberdeen City" and "AB12 3 (part) Aberdeenshire".) To convert these to coordinates, I stripped off any "(part)" information, and took the arithmetic mean of easting and northing coordinates for all postal codes that matched the pattern (257 of them in the case of AB12 3). 1,012 postcode sectors were listed, covering 5,295,403 people, and I was able to determine coordinates for all of them.

(If five million people deserve their own parliament without outside interference, why can't we have home rule for England?)

I don't have data for the Isle of Man, the Channel Islands, or anything else outside England, Scotland and Wales. But Berwick-upon-Tweed (TD15) is included in the data for England and Wales.

This process gave me a list of easting and northing coordinates with a population for each: a total of 1,303,474 points. The next step was to work out the actual centre of population. There are several different ways of doing this (see Wikipedia for more).

The simplest approach is the arithmetic mean centre, or centroid. This simply takes the arithmetic mean of each set of coordinates (weighted by population). If each person were the same weight, the country were a weightless plane, and one looked for the balance point, this is where it would be. The answer was E433908, N309645.

Slightly more complex is the median centre, which is defined by a pair of lines each dividing the population in half. For each coordinate axis, sort all the coordinates into order (weighted by population), then pick the value that occurs half-way along the list. The answer in this case was E434832, N291790: a quarter of the population lies in each quadrant (NE, SE, NW, SW) starting from that point. (That this is somewhat south of the centroid suggests that the northern half of the population is more spread out than the southern.)

Finally, and with highest computational complexity, is the geometric median. This is the one that makes most intuitive sense, at least to me: it is the point with the lowest value of the sum of all distances to it. (So if everyone were to set off from their homes and move in a straight line towards it, it would be the point which involved least total travel.) This had to be computed iteratively: I spread a coarse grid across the coordinate space and computed the value of sum-of-distances at each intersection, then used the intersection with the lowest value as the centre of a new and smaller grid, assuming that there would be no local minima. The answer I obtained was E441018, N288722.

These points are all within a few miles of each other, roughly between Birmingham and Leicester (which perhaps explains the NEC to some extent).

If one really wanted to be painstaking, one could derive actual travel times using a route-finding engine and try to minimise the sum of those, but this would be a hugely long process, would have significant errors where a postcode centre is in an inaccessible location, and would not account for air travel.

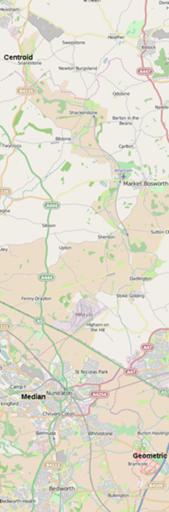
Here are the specific coordinates converted to latitude/longitude (using the full OSTN02 transformation and corrected to the WGS84 ellipsoid) as Wikimapia links (which lets you quickly switch between map and satellite imagery):

Centroid, Median, Geometric Median.