RogerBW's Blog

I’ve been doing the Weekly Challenges. The latest involved array searching and an emulated seven-segment display. (Note that this is open until the end of today.)

Goodness, challenge #200 - nearly four years since this started. The first one I did was number 14, only in Perl to start with; I might at some point go back and give the first ones the polyglot treatment. (Not to mention the "better programmer than I was then" treatment.)

Many thanks to Mohammad Anwar for keeping this going!

Task 1: Arithmetic Slices

You are given an array of integers.

Write a script to find out all Arithmetic Slices for the given array of integers.

An integer array is called arithmetic if it has at least 3 elements and the differences between any three consecutive elements are the same.

This looks as though it needs an exhaustive search. The only optimisation I put in is that if a slice (a..b) is valid, any slice that starts at a and goes on beyond b must also be valid, so we don't need to test it, just add it to the output list.

(The other approach that occurred to me after I'd written this in the usual nine languages would be to note the indices of each triplet that matches the definition, then filter all possible ranges for ones that include at least one matching triplet. Too late now.)

Rust:

fn arithmeticslices(l: Vec<isize>) -> Vec<Vec<isize>> {
    let mut o = Vec::new();
    if l.len() >= 3 {
        for a in 0..=l.len() - 3 {
            let mut valid = false;
            for b in a + 2..=l.len() - 1 {
                let mut v = vec![0; b - a + 1];
                v.copy_from_slice(&l[a..=b]);
                if !valid {
                    for i in 0..=v.len() - 3 {
                        if v[i + 1] - v[i] == v[i + 2] - v[i + 1] {
                            valid = true;
                            break;
                        }
                    }
                }
                if valid {
                    o.push(v);
                }
            }
        }
    }
    o
}

Task 2: Seven Segment 200 Submitted by: Ryan J Thompson

A seven segment display is an electronic component, usually used to display digits. The segments are labeled 'a' through 'g' as shown:

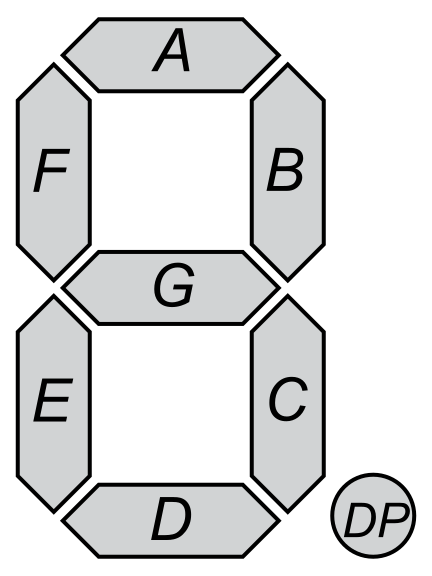
The encoding of each digit can thus be represented compactly as a truth table:

my @truth = qw<abcdef bc abdeg abcdg bcfg acdfg a cdefg abc abcdefg abcfg>;

For example, $truth[1] = 'bc'. The digit 1 would have segments 'b' and 'c' enabled.

Write a program that accepts any decimal number and draws that number as a horizontal sequence of ASCII seven segment displays, similar to the following:

-------  -------  -------
    |  |     |  |     |
    |  |     |  |     |
-------  
|        |     |  |     |
|        |     |  |     |
-------  -------  -------

To qualify as a seven segment display, each segment must be drawn (or not drawn) according to your @truth table.

The number "200" was of course chosen to celebrate our 200th week!

Rather than the provided truth table I use a bitmap table disp containing the character shapes (bit 0 being equivalent to the "a" cell, bit 1 "b", etc.; I prefer no bottom bar on the digit 9), and write each bar into cells of a string array (depending on the language, each line is either a string that I can poke at directly or more usually an array of characters that I'll combine into a string for printing).

If I were writing this for more general use I'd probably make the actual display routine take a string or array-of-digits input, and separate out the number-to-string conversion, so that I could also show hex digits (bitmap values 0x77, 0xfc, 0x39, 0x5e, 0x79, 0x71). Also perhaps separate the bitmap lookups and the segment drawing, with an intermediary array of bitmaps, to allow for multiple output formats.

Raku:

sub sevensegment($l) {
    my @disp = (0x3f, 0x06, 0x5b, 0x4f, 0x66, 0x6d, 0x7d, 0x07, 0x7f, 0x67);
    my @v;
    if ($l == 0) {
        @v.push(0);
    } else {
        my $ll = $l;
        while ($ll > 0) {
            @v.push($ll % 10);
            $ll div= 10;
        }
        @v = @v.reverse;
    }
    my @d = [" " xx 6 * @v.elems] xx 7;
    for (@v.kv) -> $i, $vv {
        my $x = 6 * $i;
        my $da = @disp[$vv];
        if ($da +& 1 > 0) {
            for ($x + 1..$x + 3) -> $xa {
                @d[0][$xa] = '#';
            }
        }
        if ($da +& 2 > 0) {
            for (1..2) -> $y {
                @d[$y][$x + 4] = '#';
            }
        }
        if ($da +& 4 > 0) {
            for (4..5) -> $y {
                @d[$y][$x + 4] = '#';
            }
        }
        if ($da +& 8 > 0) {
            for ($x + 1..$x + 3) -> $xa {
                @d[6][$xa] = '#';
            }
        }
        if ($da +& 16 > 0) {
            for (4..5) -> $y {
                @d[$y][$x] = '#';
            }
        }
        if ($da +& 32 > 0) {
            for (1..2) -> $y {
                @d[$y][$x] = '#';
            }
        }
        if ($da +& 64 > 0) {
            for ($x + 1..$x + 3) -> $xa {
                @d[3][$xa] = '#';
            }
        }
    }
    for (@d) -> @r {
        say @r.join('');
    }
}

which produces

 ###   ###   ###
    # #   # #   # 
    # #   # #   # 
 ###
#     #   # #   # 
#     #   # #   # 
 ###   ###   ###

Now I'm remembering fourteen- and sixteen-segment alphanumeric displays…

Full code on github.