RogerBW's Blog

Sometimes my interests intersect. I've been working on a way to plot markers and objects onto real-world charts.

The charts in question are the Tactical Pilotage Charts (1:500,000) and Operational Navigation Charts (1:1,000,000); these are used for civilian and some military air navigation, and so focus on terrain altitudes and features recognisable from the air. Current charts are vastly expensive, but a fairly complete set from the late 1980s and early 1990s is available from the Map Collection of the Perry-Castañeda Library at the University of Texas: here are the TPCs, and here are the ONCs.

I'm going to go into a fair bit of technical detail, but first: why am I doing this? (Beyond the obvious: for playing Harpoon or other games, e.g. by email, with limited information available to the players.) Two reasons. One is to use real world locations with some degree of accuracy; while many published scenarios for Harpoon are set in generic open sea, quite a few are not. A scenario map, such as the ones found in this PDF, tends to be a pretty rough affair, and is hard to translate into something directly gameable, whereas with the charts one can get a much greater degree of detail. The other reason is visual appeal, and this is why I'm using these particular charts rather than tiles from OpenStreetMap (which would be much simpler as there's continuous world-wide coverage, so I wouldn't need to think about individual map sheets): the aviation charts "feel" more relevant to the situation than a general-purpose map. (Maritime charts would be even better, of course, but there's no free source for those that I'm aware of, and many areas aren't covered at all.)

The scans aren't perfect; there are places where what should be straight lines suddenly jump sideways an arcminute or two, presumably because of a crease or tear in the original. But they're decently high resolution, to the point where a single map sheet can be around sixteen megabytes in size and 9000×6000 pixels. (Fortunately for a modern computer it's generally not a problem to view an image this large in a web browser, either zoomed out to get a general impression or zoomed in to view detail.) The full TPC set is around ten gibibytes, while the ONC set is about 3.4. Another downside is that there are no charts of areas that contain no land.

Also, these don't use a simple projection. They work on the Lambert conformal conic projection, and coping with that is what the meat of this post is about. I wrote my code in Perl, but I'll avoid specificities of programming language here.

This projection shows parallels of latitude as curved lines, and parallels of longitude as straight lines. I therefore made a simplifying abstraction: I treat the LCC as a form of polar coordinates, where latitude is the distance r from the north pole and longitude is the angle θ from some arbitrary meridian. There's some error in the longitude conversion by using this method, but it's less than the errors already in the scan.

This then is the basis for the conversion. I measure four points on the map, three along a parallel of latitude (conventionally the edge nearest the pole) and one along a (conventionally leftmost) parallel of longitude, and store both their latitude and longitude (read from the map) and their pixel x and y coordinates.

From the points at the same latitude, I generate the pixel coordinates xc and yc of the centre of the latitude circle (where the pole would be, if one were foolish enough to extend this map that far); this is of course a long way off the actual map. There are multiple methods for doing this, and your language's geometry library may already have one; failing that, either take the perpendicular bisectors of the lines between two of the pairs of points and find their intersection, or generate three simultaneous equations of the form (xn-xc)²+(yn-yc)²=R², where (xn,yn) are individual points on the circumference, and solve for R, xc and yc.

Then it's just a matter of generating linear conversions (of the form y=a+bx): one converts latitude in degrees to the r distance in pixels from the virtual pole (based on first and fourth points), while the other converts longitude in degrees to a useful θ, based on first and third points. At this point plotting a latitude/longitude location becomes a simple matter of converting polar to Cartesian coordinates (and of course the process is reversible).

I've played a fair bit of computer Harpoon, so I plot with the NTDS symbology, more or less as seen here, though I don't use the "carrier" symbol. It's fairly easy to pick up, and at least mildly authentic.

So here is HMS Coventry in San Carlos Water, coming under attack by a pair of Skyhawks. The heavy circles on land are small airfields.

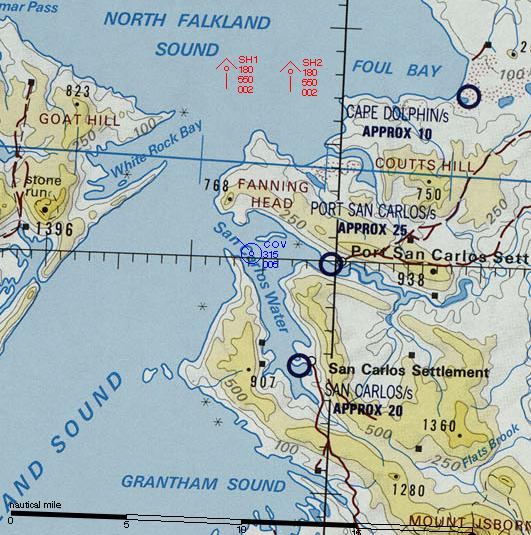
Everything that gets plotted on the map is defined in terms of latitude and longitude coordinates rather than X and Y. This makes calculations of ranges and bearings somewhat more involved, but for Perl at least there's the excellent Geo::Ellipsoid module that does all the heavy lifting.

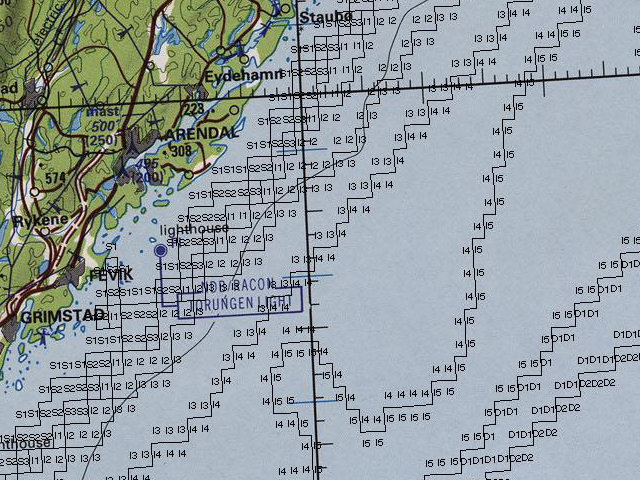
Since Harpoon gaming often involves submarines, I was very happy to find the ETOPO1 dataset from the NOAA. This is a free, arcminute-resolution, data set of global elevations, including sea depths. It's not perfect, but it's a usable abstraction that's easy to add to a map plot (here I'm converting depth to Harpoon's bands, off the southern coast of Norway in the midst of the Skagerrak).

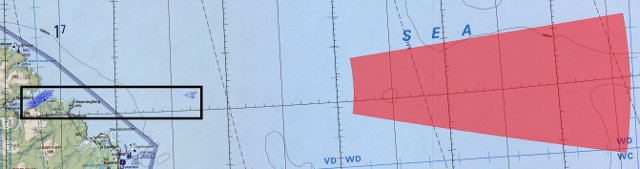
It's also possible to plot circles, boxes, and arbitrary paths (which can include arc segments as well as straight lines). Here's a setup map for the Battles of the Third World War scenario The Russians Are Coming, where the Russian start zone in the Barents Sea is described as "from 30 to 80 nautical miles from [the Norwegian ship Nordkapp], between bearings 080 and 100". (The black box surrounds all units that a player knows about, his own and any detected enemies, and is used as an aid for getting one's bearings on the full map.) Click image for full-size view.