RogerBW's Blog

I’ve been doing the Perl Weekly Challenges. The latest involved file analysis and combinatorial explosion. (Note that this is open until 20 June 2021.)

TASK #1 › Missing Row

You are given text file with rows numbered 1-15 in random order but there is a catch one row in missing in the file.

11, Line Eleven [etc.]

Write a script to find the missing row number.

I assume that any row which starts with a number is the row of that number. The filename is the parameter to my function. This basically happens in two stages:

1. read each line, find the number, list that as "a number which is not missing"
2. look for each positive integer in that list of non-missing numbers, return for the first one which isn't there.

Here's the Raku:

sub mr($n) {
  my $f=SetHash.new;
  my $fh=open :r,$n or die "Cant open file\n";
  for $fh.lines {
    .chomp;
    if (/^(<[0..9]>+)/) {
      $f{$0+0}=1;
    }
  }
  my $a=1;
  while (1) {
    unless ($f{$a}:exists) {
      return $a;
    }
    $a++;
  }
}

You could probably do something clever with first but I didn't.

This version finds the first missing number from 1 up, however large the file; a more sophisticated but less general approach would be to assume that the missing number isn't the first or the last, and look for gaps between the found numbers. Or just start with a set of 1..15 and delete rows as observed.

TASK #2 › Find Possible Paths

You are given size of a triangle.

Write a script to find all possible paths from top to the bottom right corner.

In each step, we can either move horizontally to the right (H), or move downwards to the left (L) or right (R). BONUS: Try if it can handle triangle of size 10 or 20.

Since I'm required to find the paths, not just return a count of them, I'll use my standard non-recursive search pattern. (I looked at ways of mutating the always-valid solution of R×n, but it seemed too much like work.)

Each entry in chain is a tuple of (string of path so far, x position, y position). (Except in Raku where I couldn't get it to do a list of lists, so I used a list of hashes. But this is the first time I've explicitly used the "tuple" type in Rust.) My x and y are slightly unexpected, though. Here's my coordinate system for n=2:

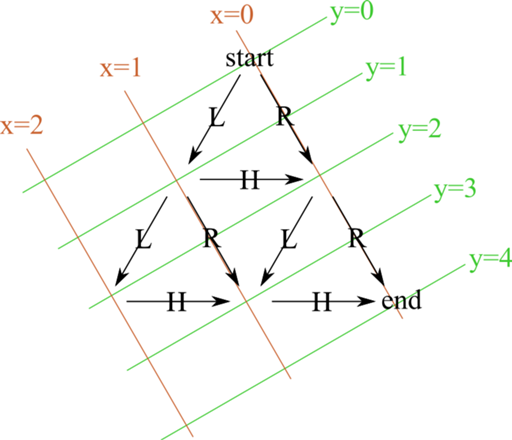
(First time I've used a diagram in a PWC blog post…)

Each valid path starts at (0,0) and ends at (0,4). Each node can generate up to three new path entries. For the y value reachable from the current node, I work out the maximum possible x (the minimum is always 0), and add the path entries that will remain within those bounds. Here's the Ruby version:

def fpp(n)
  o=Set.new
  chain=[["",0,0]]

lim is the maximum y value, which goes up by 4 per +1 except that n=1 has a maximum y of 2.

  lim=(n-1)*4
  if n==1 then
    lim=2
  end
  while chain.length() > 0
    p=chain.pop

These are just convenience aliases.

    x=p[1]
    y=p[2]

If we have a valid solution, add it to the solution set.

    if y >= lim then
      o.add(p[0])
    else

Otherwise, work out the maximum x for the next row.

      mxx=y+1
      if y >= n then
        mxx=lim-y-1
      end

And then for each direction, H, R and L, see if it fits, then generate the path and add it. (There's a bug here - when I'm going to y+2 I should really use a different mxx value because it's one row further down. But it works anyway, because an R-path can only exist where an L-path is possible.)

      0.upto(2) do |txi|
        tx=x-1+txi
        if tx>=0 && tx<=mxx then
          if txi==0 then
            chain.push([p[0]+'H',x-1,y+1])
          elsif txi==1 then
            chain.push([p[0]+'R',x,y+2])
          else
            chain.push([p[0]+'L',x+1,y+1])
          end
        end
      end
    end
  end

Then get the result set, and sort it (because I also sort the test-case answers for easy verification).

  return o.to_a.sort
end

The number of possible paths for each size is in the OEIS, except for the first term, and that gives a formula to generate it. (Interesting that that's every second value of another sequence which gives the number of routes across a square grid allowing diagonal movement.)

sub fpp {
  my $n=shift;
  my $s=0;
  foreach my $i (0..$n*2) {
    $s+=ncr(2*$n+1,$i+1)*ncr(2*$n+$i,$i);
  }
  $s/=(2*$n+1);
  return $s;
}

(ncr is the number of r-combinations to be made out of n, the usual n!/r!(n-r)! for which the actual functions are quite standard or may be available in libraries. I used Memoize a lot.)

Full code on github.