I've been adminisitering a hidden-movement game over at the tekeli.li
forums, and it occurred to me that this was a potentially enjoyable
programming challenge.
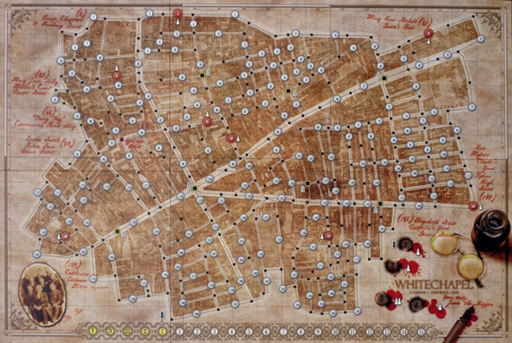
The game in question is Letters from
Whitechapel,
though the analysis would also apply to its smaller cousin Whitehall
Mystery.
In each game, a killer (known as "Jack", because LfW is themed after
the Jack the Ripper murders) must travel from place to place, while a
number of investigators try to track him down. Fine details vary
between the games, but broadly Jack takes a move (possibly using one
of a limited number of special move cards) from one map circle to
another, after which the investigators move on the black squares and
search adjacent circles for signs of Jack's passage.
So I thought I'd take a look at the computing possibilities. I wrote
an analyser which is fed the public information: when and how Jack has
moved, how the investigators move, where they search and with what
result. (Also someone has very kindly typed in all the coordinates and
connections for the Whitechapel map; there's a file on BGG. Not yet
for Whitehall, though I'm working on it.)
The actual geometry doesn't matter, so one can model the connections
as a topological map. Here's a subset of that (using GraphViz).

It's all a bit brute force. Say Jack strikes at 132, then makes a
regular move. Assuming there are no investigators nearby, there are
nine nodes he could reach: 92, 106, 107, 108, 109, 110, 131, 133,
or 134. (Jack cannot choose to remain in place, though a later move
can revisit a node visited earlier.) So the "Jack list" consists of
nine trails: [132, 92], [132, 106], and so on. If investigators are
nearby, this list will be shorter as Jack can't move through them, so
those trails don't get added to the list of possibilities. Other
options are a carriage move (two moves in one, and can move through
investigators, but still can't end up where it started) and an alley
move (in effect accessing a different network, moving to a different
point on the edge of an enclosed area). In Whitehall Mystery there's
also the possibility of a boat move, which is in effect a sort of
alley move that uses yet a third network. The investigators are told
what sort of special move was used, or that none at all was used, but
that's all they have to go on.
On Jack's next move, each chain gets all possible moves appended to
it; so [132, 92] would be replaced by the larger set [132, 92, 75].
[132, 92, 90], etc.
Investigators moving add no information (but have to be tracked, as
they restrict Jack's future moves). When the investigators search,
though, the list of possible trails is pruned: a negative search
removes all trails that have that node on them, while a positive
search removes all trails that don't. A successful arrest wins the
game, but an unsuccessful arrest only tells you that that location is
not the end of Jack's trail. It's interesting to note that game at
the table tends to promote the view of a negative search as a failure,
while in fact it can eliminate a whole sheaf of possibilities that
could only have been reached by going via that node.
In the recent game I've seen situations with a search space of 12,000
or more paths to 43 possible locations—but obviously that's well
within the bounds of the machine to keep track of, if rather beyond
what a human would be likely to manage.
That will tell me about possible locations, the tail nodes of all the
paths, but what more can one do? I added a heuristic:
For each node that might possibly be on a trail, and hasn't already
been found to have a clue in it (i.e. is potentially worth searching),
look at the set of paths to each tail node. If all of them or none of
them pass through the candidate node, the node has some segmentation
power: if I search in this particular node, I can reduce the set of
possible tail nodes. The score I assign to this node is the number of
tail nodes excluded, multiplied by the number included, which is
perhaps perverse: don't I want to reduce the tail nodes as much as
possible? Yes, but I don't know whether the search will produce a clue
or not, so I'd rather make a search that will slice the node set in
half whether there's a clue or not than one that will pin down Jack if
there is a clue but leave many other possible nodes if there isn't.
I wrote all this in Crystal, mostly because it seemed like fun: it's
easier to get up and running quickly than Rust, I didn't expect to
need any external libraries (as indeed I didn't), and it's pleasingly
fast. It's particularly interesting to notice when a search reveals
that there's only one possible place where Jack can be right now,
since all other possibilities have been eliminated by one means or
another—which of course one wouldn't notice at the table unless one
were trying to model a similar process.
Is this a good thing for the game? Absolutely not; I've held back
posting this until the game was over. In order to be enjoyable, the
game relies on the fallibility of human memory, and although the
software isn't directly suggesting an optimal strategy it can simply
keep track of things far more effectively than any unassisted player
could.
Comments on this post are now closed. If you have particular grounds for adding a late comment, comment on a more recent post quoting the URL of this one.