It has been established that no more than four colours are necessary
to colour regions of a map with no adjacent regions the same colour.
But hoe does one actually go about doing this?
I'm using the "map" puzzle from Simon Tatham's puzzle collection;
you can play that
here,
though the example screenshots are from an Android
implementation.
Solid regions are known to be a colour; dots are added manually to
indicate that this colour is possible for that region.
The most obvious approach is that if a region has three distinct
neighbour colours it must take on the fourth one.
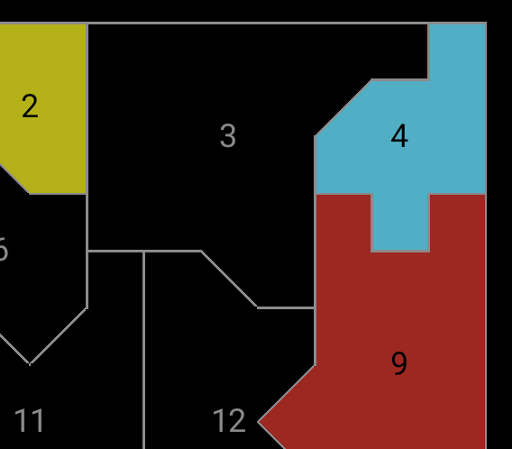
Here, since regions 2, 4 and 9 are distinct and all adjoin region 3, 3
must be in the fourth colour (green). That's enough logic for many
Easy puzzles.
The doubled pair approach needs two unknown regions, touching each
other and a third region, constrained to the same two colours.
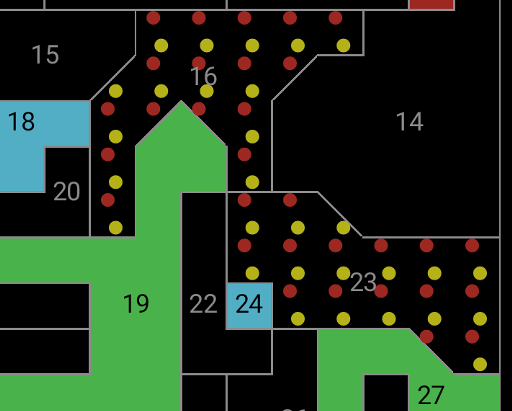
Here, 19 and 18 both touch 16, so 16 can only be red or yellow. 24 and
27 both touch 23, so it is similarly constrained. 16 and 23 touch each
other, so they can't be the same colour; between the two of them there
must be one red and one yellow.
Therefore region 14 can't be either red or yellow, and must be green
or blue. (And if it were next to a green, it would definitely be
blue.) This is generally enough logic for Normal mode.
The same principle can be extended with any even-length chain of
regions:
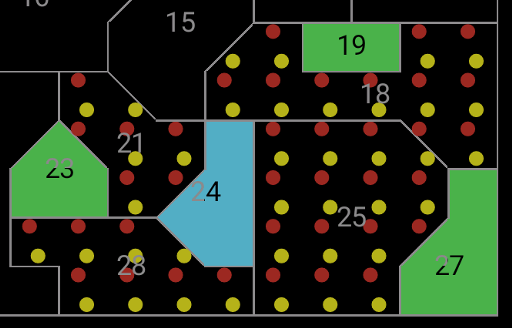
Here, 23 and 4 make 21 and 28 red/yellow; 27 and 4 make 25
red/yellow; and 4 and 19 make 18 red/yellow. So the four rejoins must
either be red-yellow-red-yellow or yellow-red-yellow-red; and either
way, region 15 must be blue or green.
Finally of the tricks I've found, a different sort of constraint.
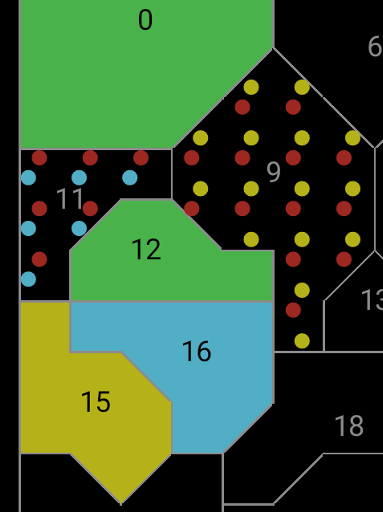
0/12 and 15 constrain 11 to be red or blue. 0/12 and 16 constrain 9 to
be red or yellow.
But up to and including Hard mode, we are told that the map must be
solvable by logic without trial and error. If 9 were yellow, then 11
would be entirely surrounded by green and yellow, and it could be
either red or blue with no way to decide between them, which is an
invalid configuration. Therefore 9 must be red, which forces 11 to be
blue.
That's clearly not all the necessary logic; it's not enough to solve
all Hard puzzles without occasionally guessing and backtracking. Is
this something that's been written about elsewhere? Searching mostly
finds proofs that four-colouring is possible, which is fair enough,
but not what I'm after…